Метод Монте-Карло относится к методам __________ моделирования. Моделирование методом монте-карло Метод монте карло численный решения

методом Монте – Карло

1. Предмет метода Монте-Карло

Датой рождения метода Монте – Карло принято считать 1949 год, когда учёные Н. Метрополис и С.Улам опубликовали статью под названием «Метод Монте – Карло», в которой изложили суть своего метода. Название метода связано с названием города Монте – Карло, где в игорных домах (казино) играют в рулетку, которая является одним из простейших устройств для получения, так называемых, «случайных чисел », на использование которых основан данный метод.

ЭВМ позволяют легко получать, так называемые, «псевдослучайные числа » (при решении задач их часто применяют вместо случайных чисел). Это привело к широкому внедрению метода во многие области науки и техники (статистическая физика, теория массового обслуживания, теория игр и др.). Метод Монте – Карло используют для вычисления интегралов, в особенности многомерных, для решения систем алгебраических уравнений высокого порядка, для исследования различного рода сложных систем (автоматического управления, экономических, биологических и т.д.).

Сущность метода Монте – Карло состоит в следующем:требуется найти значение числа некоторой изучаемой величины. Для этого выбирают такую случайную величину
, математическое ожидание которой равно:
, т.е. решит указанное функциональное уравнение. Эта задача в общем случае весьма сложная и трудная.

Практически же поступают так: производят испытаний, в результате которых получаютвозможных значений
; вычисляют их среднее арифметическое

и принимают в качестве оценки (приближённого значения)искомого числа:

Поскольку метод Монте – Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний . Теория этого метода указывает, как наиболее целесообразно выбрать случайную величину
, как найти её возможные значения. В частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания числаего оценкой.

Отыскание возможных значений случайной величины
(моделирования) называют «разыгрыванием случайно величины ». Здесь мы изложим лишь некоторые способы разыгрывания с.в.
и укажем, как оценить допускаемую при этом ошибку.

2. Случайные числа, оценка погрешности метода Монте – Карло.

Как уже отметили, метод Монте – Карло основан на применении случайных чисел; приведём определение этих чисел. Обозначим через н.с.в., распределённую равномерно в интервале
.

Случайными числами называют возможные значения непрерывной случайной величины, распределённой равномерно в интервале
.

В действительности пользуются неравномерно распределённой с.в. , возможные значения которой, вообще говоря, имеют бесконечное число десятичных знаков, аквазиравномерной случайно величиной
, возможное значение которой имеют конечное число знаков. В результате заменына
разыгрываемая величина имеет не точно, а приближённо заданное распределение.

В конце книги приведена таблица случайных чисел, заимствованную из книги (Большев Л.Н….»Таблицы математической статистики. Наука, 1965г.).

Пусть для получения оценки математического ожидания числаслучайной величины
было произведенонезависимых испытаний (разыграновозможных значений) и по ним была найдена выборочная средняя, которая принята в качестве искомой оценки
.

Ясно, что, если повторить опыт, то будут получены другие возможные значения
. Следовательно, другая средняя и другая оценка числа
. Уже отсюда следует, что получит в общем случае точную оценку МО невозможно.

Естественно, возникает вопрос о величине допускаемой ошибки. Ограничимся здесь отысканием лишь верхней границы допускаемой ошибки с заданной вероятностью (надёжностью)

Интересующая нас верхняя граница ошибки есть не что иное, как «точность оценки » математического ожидания по выборочной средней при помощи доверительных интервалов уже шла речь в разделе дополнение1, тема 21. В связи с этим воспользуемся полученные ранее

Не так давно я прочитал замечательную книгу Дугласа Хаббарда . В кратком конспекте книги я обещал, что одному из разделов – Оценка риска: введение в моделирование методом Монте-Карло – я посвящу отдельную заметку. Да всё как-то не складывалось. И вот недавно я стал более внимательно изучать методы управления валютными рисками. В материалах, посвященных этой тематике, часто упоминается моделирование методом Монте-Карло. Так что обещанный материал перед вами.

Приведу простой пример моделирования методом Монте-Карло для тех, кто никогда не работал с ним ранее, но имеет определенное представление об использовании электронных таблиц Excel.

Предположим, что вы хотите арендовать новый станок. Стоимость годовой аренды станка 400 000 дол., и договор нужно подписать на несколько лет. Поэтому, даже не достигнув , вы всё равно не сможете сразу вернуть станок. Вы собираетесь подписать договор, думая, что современное оборудование позволит сэкономить на трудозатратах и стоимости сырья и материалов, а также считаете, что материально-техническое обслуживание нового станка обойдется дешевле.

Скачать заметку в формате , примеры в формате

Ваши калиброванные специалисты по оценке дали следующие интервалы значений ожидаемой экономии и годового объема производства:

Годовая экономия составит: (MS + LS + RMS) х PL

Конечно, этот пример слишком прост, чтобы быть реалистичным. Объем производства каждый год меняется, какие-то затраты снизятся, когда рабочие окончательно освоят новый станок, и т.д. Но мы в этом примере намеренно пожертвовали реализмом ради простоты.

Если мы возьмем медиану (среднее) каждого из интервалов значений, то получим годовую экономию: (15 + 3 + 6) х 25 000 = 600 000 (дол.)

Похоже, что мы не только добились безубыточности, но и получили кое-какую прибыль, но не забывайте – существуют неопределенности. Как же оценить рискованность этих инвестиций? Давайте, прежде всего, определим, что такое риск в данном контексте. Чтобы получить риск, мы должны наметить будущие результаты с присущими им неопределенностями, причем какие-то из них – с вероятностью понести ущерб, поддающийся количественному определению. Один из способов взглянуть на риск – представить вероятность того, что мы не добьемся безубыточности, то есть что наша экономия окажется меньше годовой стоимости аренды станка. Чем больше нам не хватит на покрытие расходов на аренду, тем больше мы потеряем. Сумма 600 000 дол. – это медиана интервала. Как определить реальный интервал значений и рассчитать по нему вероятность того, что мы не достигнем точки безубыточности?

Поскольку точные данные отсутствуют, нельзя выполнить простые расчеты для ответа на вопрос, сможем ли мы добиться требуемой экономии. Есть методы, позволяющие при определенных условиях найти интервал значений результирующего параметра по диапазонам значений исходных данных, но для большинства проблем из реальной жизни такие условия, как правило, не существуют. Как только мы начинаем суммировать и умножать разные типы распределений, задача обычно превращается в то, что математики называют неразрешимой или не имеющей решения обычными математическими методами проблемой. Поэтому взамен мы пользуемся методом прямого подбора возможных вариантов, ставшим возможным благодаря появлению компьютеров. Из имеющихся интервалов мы выбираем наугад множество (тысячи) точных значений исходных параметров и рассчитываем множество точных значений искомого показателя.

Моделирование методом Монте-Карло – превосходный способ решения подобных проблем. Мы должны лишь случайным образом выбрать в указанных интервалах значения, подставить их в формулу для расчета годовой экономии и рассчитать итог. Одни результаты превысят рассчитанную нами медиану 600 000 дол., а другие окажутся ниже. Некоторые будут даже ниже требуемых для безубыточности 400 000 дол.

Вы легко сможете осуществить моделирование методом Монте-Карло на персональном компьютере с помощью программы Excel, но для этого понадобится чуть больше информации, чем 90%-ный доверительный интервал. Необходимо знать форму кривой распределения. Для разных величин больше подходят кривые одной формы, чем другой. В случае 90%-ного доверительного интервала обычно используется кривая нормального (гауссова) распределения. Это хорошо знакомая всем колоколообразная кривая, на которой большинство возможных значений результатов группируются в центральной части графика и лишь немногие, менее вероятные, распределяются, сходя на нет к его краям (рис. 1).

Вот как выглядит нормальное распределение:

Рис.1. Нормальное распределение. По оси абсцисс число сигм.

Особенности:

• значения, располагающиеся в центральной части графика, более вероятны, чем значения по его краям;
• распределение симметрично; медиана находится точно посредине между верхней и нижней границами 90%-ного доверительного интервала (CI);
• «хвосты» графика бесконечны; значения за пределами 90%-ного доверительного интервала маловероятны, но все же возможны.

Для построения нормального распределения в Excel можно воспользоваться функцией =НОРМРАСП(Х; Среднее; Стандартное_откл; Интегральная), где
Х – значение, для которого строится нормальное распределение;
Среднее – среднее арифметическое распределения; в нашем случае = 0;
Стандартное_откл – стандартное отклонение распределения; в нашем случае = 1;
Интегральная – логическое значение, определяющее форму функции; если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения; в нашем случае = ЛОЖЬ.

Говоря о нормальном распределении, необходимо упомянуть о таком связанном с ним понятии, как стандартное отклонение. Очевидно, не все обладают интуитивным пониманием, что это такое, но поскольку стандартное отклонение можно заменить числом, рассчитанным по 90%-ному доверительному интервалу (смысл которого интуитивно понимают многие), я не буду здесь подробно на нем останавливаться. Рисунок 1 показывает, что в одном 90%-ном доверительном интервале насчитывается 3,29 стандартного отклонения, поэтому нам просто нужно будет сделать преобразование.

В нашем случае следует создать в электронной таблице генератор случайных чисел для каждого интервала значений. Начнем, например, с MS – экономии на материально-техническом обслуживании. Воспользуемся формулой Excel: =НОРМОБР(вероятность;среднее;стандартное_откл), где
Вероятность – вероятность, соответствующая нормальному распределению;
Среднее – среднее арифметическое распределения;
Стандартное_откл – стандартное отклонение распределения.

В нашем случае:
Среднее (медиана) = (Верхняя граница 90%-ного CI + Нижняя граница 90%-ного СI)/2;
Стандартное отклонение = (Верхняя граница 90%-ного CI – Нижняя граница 90%-ного СI)/3,29.

Для параметра MS формула имеет вид: =НОРМОБР(СЛЧИС();15;(20-10)/3,29), где
СЛЧИС – функция, генерирующая случайные числа в диапазоне от 0 до 1;
15 – среднее арифметическое диапазона MS;
(20-10)/3,29 = 3,04 – стандартное отклонение; напомню, что смысл стандартного отклонения в следующем: в интервал 3,29*Стандарт_откл, расположенный симметрично относительного среднего, попадает 90% всех значений случайной величины (в нашем случае MS)

Распределение величины экономии на материально-техническом обслуживании для 100 случайных нормально распределенных значений:

Рис. 2. Вероятность распределения MS по диапазонам значений; о том, как построить такое распределение с помощью сводной таблицы см.

Поскольку мы использовали «лишь» 100 случайных значений, распределение получилось не таким уж и симметричным. Тем не менее, около 90% значений попали в диапазон экономии на MS от 10 до 20 долл. (если быть точным, то 91%).

Построим таблицу на основе доверительных интервалов параметров MS, LS, RMS и PL (рис. 3). Два последних столбца показывают результаты расчетов на основе данных других столбцов. В столбце «Общая экономия» показана годовая экономия, рассчитанная для каждой строки. Например, в случае реализации сценария 1 общая экономия составит (14,3 + 5,8 + 4,3) х 23 471 = 570 834 долл. Столбец «Достигается ли безубыточность?» вам на самом деле не нужен. Я включил его просто для информативности. Создадим в Excel 10 000 строк-сценариев.

Рис. 3. Расчет сценариев методом Монте-Карло в Excel

Чтобы оценить полученные результаты, можно использовать, например, сводную таблицу, которая позволяет подсчитать число сценариев в каждом 100-тысячном диапазоне. Затем вы строите график, отображающий результаты расчета (рис. 4). Этот график показывает, какая доля из 10 000 сценариев будут иметь годовую экономию в том или ином интервале значений. Например, около 3% сценариев дадут годовую экономию более 1М дол.

Рис. 4. Распределение общей экономии по диапазонам значений. По оси абсцисс отложены 100-тысячные диапазоны размера экономии, а по оси ординат доля сценариев, приходящихся на указанный диапазон

Из всех полученных значений годовой экономии примерно 15% будут меньше 400К дол. Это означает, что вероятность ущерба составляет 15%. Данное число и представляет содержательную оценку риска. Но риск не всегда сводится к возможности отрицательной доходности инвестиций. Оценивая размеры вещи, мы определяем ее высоту, массу, обхват и т.д. Точно так же существуют и несколько полезных показателей риска. Дальнейший анализ показывает: есть 4%-ная вероятность того, что завод вместо экономии будет терять ежегодно по 100К дол. Однако полное отсутствие доходов практически исключено. Вот что подразумевается под анализом риска – мы должны уметь рассчитывать вероятности ущерба разного масштаба. Если вы действительно измеряете риск, то должны делать именно это.

В некоторых ситуациях можно пойти более коротким путем. Если все распределения значений, с которыми мы работаем, будут нормальными и нам надо просто сложить интервалы этих значений (например, интервалы затрат и выгод) или вычесть их друг из друга, то можно обойтись и без моделирования методом Монте-Карло. Когда необходимо суммировать три вида экономии из нашего примера, следует провести простой расчет. Чтобы получить искомый интервал, используйте шесть шагов, перечисленных ниже:

1) вычтите среднее значение каждого интервала значений из его верхней границы; для экономии на материально-техническом обслуживании 20 – 15 = 5 (дол.), для экономии на трудозатратах – 5 дол. и для экономии на сырье и материалах – 3 дол.;

2) возведите в квадрат результаты первого шага 5 2 = 25 (дол.) и т.д.;

3) суммируйте результаты второго шага 25 + 25 + 9 = 59 (дол.);

4) извлеките квадратный корень из полученной суммы: получится 7,7 дол.;

5) сложите все средние значения: 15 + 3 + 6 = 24 (дол.);

6) прибавьте к сумме средних значений результат шага 4 и получите верхнюю границу диапазона: 24 + 7,7 = 31,7 дол.; вычтите из суммы средних значений результат шага 4 и получите нижнюю границу диапазона 24 – 7,7 = 16,3 дол.

Таким образом, 90%-ный доверительный интервал для суммы трех 90%-ных доверительных интервалов по каждому виду экономии составляет 16,3–31,7 дол.

Мы использовали следующее свойство: размах суммарного интервала равен квадратному корню из суммы квадратов размахов отдельных интервалов .

Иногда нечто похожее делают, суммируя все «оптимистические» значения верхней границы и «пессимистические» значения нижней границы интервала. В данном случае мы получили бы на основе наших трех 90%-ных доверительных интервалов суммарный интервал 11–37 дол. Этот интервал несколько шире, чем 16,3–31,7 дол. Когда такие расчеты выполняются при обосновании проекта с десятками переменных, расширение интервала становится чрезмерным, чтобы его игнорировать. Брать самые «оптимистические» значения для верхней границы и «пессимистические» для нижней – все равно что думать: бросив несколько игральных костей, мы во всех случаях получим только «1» или только «6». На самом же деле выпадет некое сочетание низких и высоких значений. Чрезмерное расширение интервала – распространенная ошибка, которая, несомненно, часто приводит к принятию необоснованных решений. В то же время описанный мной простой метод прекрасно работает, когда у нас есть несколько 90%-ных доверительных интервалов, которые необходимо суммировать.

Однако наша цель не только суммировать интервалы, но и умножить их на объем производства, значения которого также даны в виде диапазона. Простой метод суммирования годится только для вычитания или сложения интервалов значений.

Моделирование методом Монте-Карло требуется и тогда, когда не все распределения являются нормальными. Хотя другие типы распределений не входят в предмет данной книги, упомянем о двух из них - равномерном и бинарном (рис. 5, 6).

Рис. 5. Равномерное распределение (не идеальное, а построенное с помощью функции СЛЧИС в Excel)

Особенности:

• вероятность всех значений одинакова;
• распределение симметрично, без перекосов; медиана находится точно посредине между верхней и нижней границами интервала;
• значения за пределами интервала невозможны.

Для построения данного распределения в Excel была использована формула: СЛЧИС()*(UB – LB) + LB, где UB – верхняя граница; LB – нижняя граница; с последующим разбиением всех значений на диапазоны с помощью сводной таблицы.

Рис. 6. Бинарное распределение (распределение Бернулли)

Особенности:

• возможны только два значения;
• существует единственная вероятность одного значения (в данном случае 60%); вероятность другого значения равна единице минус вероятность первого значения

Для построения случайного распределения данного вида в Excel использовалась функция: =ЕСЛИ(СЛЧИС()<Р;1;0), где Р - вероятность выпадения «1»; вероятность выпадения «0» равна 1–Р; с последующим разбиением всех значений на два значения с помощью сводной таблицы.

Метод впервые использовал математик Станислав Улам (см. ).

Дуглас Хаббард далее перечисляет несколько программ, предназначенных для моделирования методом Монте-Карло. Среди них и Crystal Ball компании Decisioneering, Inc, Денвер, штат Колорадо. Книга на английском языке была издана в 2007 г. Сейчас же эта программа принадлежит уже Oracle . Демо-версия программы доступна для скачивания с сайта компании. О ее возможностях мы и погорим .

См. главу 5 упоминавшейся книги Дугласа Хаббарда

Здесь Дуглас Хаббард под размахом понимает разность между верхней границей 90%-ного доверительного интервала и средним значением этого интервала (или между средним значением и нижней границей, так как распределение симметрично). Обычно под размахом понимают разность между верхней и нижней границами.

Методы Монте-Карло используются в основном для вычисления кратных интегралов. В принципе такие интегралы можно вычислить и повторным применением выше изложенных методов. Однако с повышением кратности интеграла резко возрастает объем вычислительной работы. Методы статистических испытаний (методы Монте-Карло) свободны от этого недостатка, хотя и обеспечивают сравнительно невысокую точность. Существует большое количество вариантов этих методов. Рассмотрим два из них.

Первый из них можно интерпретировать как статистический вариант метода прямоугольников, когда в качестве узла берется случайное число, равномерно распределенное в интервале интегрирования
. Вследствие случайности узла погрешность также будет носить случайный характер. Проведя вычислений с такими случайными узлами, усредняем результат, который и принимаем за приближенное значение интеграла,

. (5.48)

Погрешность вычисления будет уменьшаться с ростом числа используемых узлов расчета функции по закону
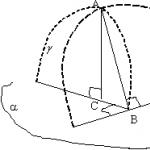
. Графическая иллюстрация метода представлена на рисунке 5.5

Рисунок 5.5. Статистический вариант метода прямоугольников

Формула (5.48) обобщается на случай кратных интегралов

Здесь
– -мерный объем области интегрирования . Число узлов, в которых необходимо вычислять подынтегральную функцию, будет пропорционально
.

Во втором варианте метода Монте-Карло интеграл приводится к виду

,(5.50)

где
находится в интервале . Тогда две случайные величины и
можно рассматривать как координаты точек в единичном квадрате (рисунок 5.8). При равномерном распределении точек в квадрате за приближенное значение интеграла принимается отношение количества точек , попавших под кривую
, к общему числу испытаний

.(5.51)

Этот алгоритм также обобщается на кратные интегралы.

Метод наименьших квадратов

Будем рассматривать систему линейных алгебраических уравнений вида

. (6.1)

Из курса линейной алгебры известно, что в том случае, когда
и число уравнений равно числу неизвестных система имеет единственное решение. На практике часто встречаются задачи, в которых либо число уравнений не совпадает с числом неизвестных, либо матрица или вектор заданы не полностью или не точно. Решение таких задач строится методом наименьших квадратов (МНК).

6.1. Решение пере- и недоопределенных слау

Задача наименьших квадратов в разных дисциплинах называется по-разному. Например, математически это есть задача отыскания для заданной точки функционального пространства ближайшей точки в заданном подпространстве. Статистика вводит в свою постановку задачи вероятностные распределения и оперирует терминами типа регрессионный анализ. Инженерный подход к решению проблемы анализа сложных систем приводит к задачам оценивания параметров или фильтрации.

Главное состоит в том, что все эти задачи содержат в себе одну и ту же центральную проблему, а именно последовательность линейных задач наименьших квадратов. Эту проблему можно сформулировать следующим образом. Пусть дана действительная
-матрица ранга
и действительный -вектор . Задача наименьших квадратов состоит в нахождении действительного -вектора , минимизирующий евклидову длину (норму) вектора невязки
.

Здесь не выдвигается никаких предположений относительно сравнительной величины параметров и , поэтому удобно все многообразие разделить на шесть случаев (рис.6.1).

В основе решения задач такого типа лежит представление
-матрицы в виде произведения
, где
и
– ортогональные матрицы. Напомним, что матрица
называется ортогональной, если
( – единичная матрица), из единственности обратной матрицы следует, что и
. Любое разложение
-матрицы такого типа называется его ортогональным разложением. Важным свойством ортогональных матриц является сохранение евклидовой длины при умножении. Это значит, что для любого -вектора и любой ортогональной
-матрицы

.(6.2)

В контексте решения задачи наименьших квадратов минимизации евклидовой нормы имеем

для произвольной ортогональной
-матрицы
и -вектора .

Использование такого разложение позволяет сформулировать задачу метода наименьших квадратов в следующем виде. Пусть – ортогональная
-матрица ранга , представленная в виде

,(6.4)

где
и
– ортогональные матрицы размерности соответственно
и
, а –
-матрица вида

,(6.5)

где
–
-матрица ранга.

Рисунок 6.1. Шесть случаев задачи МНК в соответствии со сравнительной характеристикой величин , и ранга .

Определим вектор

(6.6)

и новую переменную

(6.7)

Определим как единственное решение системы
.

, где

–произвольно. (6.8)

.(6.9)

Для нормы вектора невязки справедливо

Единственным решением минимальной длины является вектор

.(6.11)

Заменим согласно формуле (4) и получим

из уравнений (6.6)-(6.11) следует, что

для всех . Очевидно, что правая часть (6.13) имеет минимальное значение
, если

.(6.14)

Это уравнение допускает единственное решение , так как ранг
равен . Общее решение выражается формулой

,(6.15)

где произвольно. Для вектора из (6.11) имеем

, (6.16)

что устанавливает равенство (6.9). Среди векторов вида (6.15) наименьшую длину (норму) будет иметь тот, для которого
, поэтому из (6.8) получим

,(6.17)

что доказывает (6.11).

В случае
или
величины с размерностями
и
отсутствуют. В частности, при
решение задачи наименьших квадратов единственно. Отметим, что решение минимальной длины (нормы), множество всех решений и минимальное значение для нормы вектора невязки определяются единственным образом и не зависят от вида конкретного ортогонального разложения.

Для дальнейшего ограничимся несколькими утверждениями, приведенными без доказательств.

,(6.18)

где – верхняя треугольная
-матрица ранга . При этом для
-подматрицы
существует ортогональная матрица
такая, что

,

где – нижняя треугольная матрица ранга .

Первое утверждение дает возможность построить разложение матрицы в случаях
и
, где
. Действительно,
( – единичная
-матрица). Для случая
(
) запишем
или
( – единичная
-матрица). Второе утверждение дает возможность построить разложения
для случаев
-
При этом матрица представима в виде

,(6.20)

где
– невырожденная треугольная
-матрица.

Введение

Метод Монте-Карло – это численный метод решения математических задач при помощи моделирования случайных величин.

Датой рождение метода Монте-Карло принято считать 1949 г., когда появилась статья под названием «Метод Монте-Карло» (Н. Метрополис, С. Улам). Создателями этого метода считают американских математиков Дж. Неймана и С. Улама. В нашей стране первые статьи были опубликованы в 1955–56 гг. (В.В. Чавчанидзе, Ю.А. Шрейдер, В.С. Владимиров)

Однако теоретическая основа метода была известна давно. Кроме того, некоторые задачи статистики рассчитывались иногда с помощью случайных выборок, т.е. фактически методом Монте-Карло. Однако до появления ЭВМ этот метод не мог найти сколько-нибудь широкого применения, так как моделировать случайные величины вручную – очень трудоёмкая работа. Таким образом, возникновение метода Монте-Карло как весьма универсального численного метода стало возможным только благодаря появлению ЭВМ.

Само название «Монте-Карло» происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом, а одним из простейших механических приборов для получения случайных величин является рулетка.

Первоначально метод Монте-Карло использовался главным образом для решения задач нейтронной физики, где традиционные численные методы оказались малопригодными. Далее его влияние распространилось на широкий круг задач статистической физики, очень разных по своему содержанию. К разделам науки, где всё в большей мере используется метод Монте-Карло, следует отнести задачи теории массового обслуживания, задачи теории игр и математической экономики, задачи теории передачи сообщений при наличии помех и ряд других.

Метод Монте-Карло оказал и продолжает оказывать существенное влияние на развитие методов вычислительной математики и при решении многих задач успешно сочетается с другими вычислительными методами и дополняет их. Его применение оправдано в первую очередь в тех задачах, которые допускают теоретико-вероятностное описание. Это объясняется как естественность получения ответа с некоторой заданной вероятностью в задачах с вероятностным содержанием, так и существенным упрощением процедуры решения.

В подавляющем большинстве задач, решаемых методами Монте-Карло, вычисляют математические ожидания некоторых случайных величин. Так как чаще всего математические ожидания представляют собой обычные интегралы, в том числе и кратные, то центральное положение в теории методов Монте-Карло занимают методы вычисления интегралов.

1. Теоретическая часть

1.1 Сущность метода Монте-Карло и моделирование случайных величин

Предположим, что нам необходимо вычислить площадь плоской фигуры

. Это может быть произвольная фигура, заданная графически или аналитически (связная или состоящая из нескольких частей). Пусть это будет фигура, заданная на рис. 1.1.

Предположим, что эта фигура расположена внутри единичного квадрата.

Выберем внутри квадрата

случайных точек. Обозначим через число точек, попавших внутрь фигуры . Геометрически видно, что площадь фигуры приближенно равна отношению . Причем, чем больше число , тем больше точность этой оценки.

Для того чтобы выбирать точки случайно, необходимо перейти к понятию случайная величина. Случайная величина

непрерывная, если она может принимать любое значение из некоторого интервала .

Непрерывная случайная величина

определяется заданием интервала , содержащего возможные значения этой величины, и функции , которая называется плотностью вероятностей случайной величины (плотностью распределения ). Физический смысл следующий: пусть - произвольный интервал, такой что , тогда вероятность того, что окажется в интервале , равна интегралу (1.1)

Множество значений

может быть любым интервалом (возможен случай ). Однако плотность должна удовлетворять двум условиям:

1) плотность

положительна: ; (1.2)

2) интеграл от плотности

по всему интервалу равен 1: (1.3)

Математическим ожиданием непрерывной случайной величины называется число

(1.4)

Дисперсией непрерывной случайной величины называется число:

Нормальной случайной величиной называется случайная величина

, определённая на всей оси и имеющая плотность (1.5) - числовые параметры

Любые вероятности вида

легко вычисляются с помощью таблицы, в которой приведены значения функции , называемой обычно интегралом вероятностей.

Согласно (1.1)

В интеграле сделаем замену переменной

, тогда получим , Отсюда следует, что Также

Нормальные случайные величины очень часто встречаются при исследовании самых различных по своей природе вопросов.

6. Моделями типа «черный ящик являются»

1) модели мышления

2) модели, описывающие зависимость параметров состояния объекта от входных параметров

3) модели «аварийного» ящика на самолетах

4) модели, описывающие входные и выходные параметры объекта без учета внутренней структуры объекта

Определение целей моделирования осуществляется на этапе

1) разработки концептуальной модели

2) разработки математической модели

3) разработки имитационной модели

1. постановки задачи

Поставьте в соответствие друг другу определения для представленной таблицы моделирования

Среди общепринятых классификаций видов моделей отсутствует их классификация на

1) дискретные – непрерывные

2) логические – сенсорные

3) детерминированные – стохастические

1. статические – динамические

10. В отношении «объект-модель» не находятся понятия

1) микромир – квантовая механика

2) книга – абзац

3) знания – оценка

4) дом – план

Компьютерные сети

План

1. Основные понятия компьютерных сетей
2. Топология компьютерных сетей
3. Структура вычислительной сети
4. Локальные сети
5. Организация работы в локальной сети
6. Возможности сети Интернет
7. Службы Интернета
8. Сетевая операционная система
9. Тесты для самопроверки

Основные понятия компьютерных сетей

Информационно – вычислительная сеть - ИВС (часто используется название - вычислительная сеть, компьютерная сеть), представляет собой систему компьютеров, объединенных каналами передачи данных.

Канал (channel) - средство или путь, по которому передаются сигналы либо данные.

Основное назначение ИВС - обеспечение различных информационно – вычислительных услуг пользователям сети путем организации их удобного доступа к ресурсам, распределенным в этой сети. В последние годы подавляющая часть услуг сетей лежит в сфере именно информационного обслуживания. В частности, на базе ИВС обеспечивается решение следующих задач: хранение, обработка данных и передача данных и результатов обработки пользователям.

Решение этих задач обеспечивается:

• распределенными в сети аппаратными, программными и информационными ресурсами;
• дистанционным доступом пользователя к любым видам этих ресурсов;
• специализацией отдельных узлов сети на решении задач определенного класса;
• решением сложных задач совместными усилиями нескольких узлов сети.

Первые ИВС появились в 60-х годах, и это было технической революцией, сравнимой по значимости с появлением первых ЭВМ. В них была предпринята попытка объединения технологий сбора, хранения, передачи и обработки информации на ЭВМ с техникой связи.

Одной из первых сетей, оказавших влияние на дальнейшее развитие, явилась сеть АРПА. Она была создана пятидесятью университетами и фирмами США. В последнее время она охватывает всю территорию США, часть Европы и Азии. Её основное значение состоит в том, что она доказала техническую возможность и экономическую целесообразность разработки и эксплуатации больших сетей.

В 60-х годах в Европе были разработаны и внедрены международные сети EIN и Евронет, затем стали появляться национальные сети. В СССР первая сеть стала рентабельной в 60-х годах в Академии наук в Ленинграде. В 1985 г. к ней подсоединилась региональная подсеть «Северо-запад» с академическими центрами в Риге и Москве.

В 1980 г. сдана в эксплуатацию система телеобработки статистической информации (СТОСИ), обслуживающая ГВЦ ЦСУ СССР в Москве и республиканский ВЦ в союзных республиках.

В настоящее время в мире зарегистрировано более 200 глобальных сетей, (при этом более четверти из них – созданы в США). С появлением микроЭВМ и ПЭВМ появились локальные вычислительные сети (ЛВС). Объединение ЛВС с глобальными сетями позволило получить доступ к мировым информационным ресурсам.

В общем случае, для создания компьютерных сетей необходимо специальное аппаратное обеспечение (сетевое оборудование ) и специальное программное обеспечение (сетевые программные средства ).

Технология работы в сети и возникающие при этом возможности зависят как от способов организации каналов связи, так и от программного обеспечения. Можно выделить следующие виды каналов связи и организуемых с их помощью сетей.

Простейшая компьютерная сеть образуется при соединении двух недалеко отстоящих друг от друга компьютеров (в пределах 10 - 20 м) с помощью специального кабеля, называемого нуль-модемом, который подключается к последовательным или параллельным портам обоих компьютеров. Такое временное соединение называется прямым компьютерным соединением (ПКС). В настоящее время получили развитие инфракрасные порты, позволяющие организовать соединение напрямую, без кабеля. ПКС используется в основном для обмена информацией между портативным и стационарным персональным компьютером.

Локальная сеть представляет собой расположенные на небольшом расстоянии компьютеры (на удалении в пределах 50-100 м внутри одного или соседних зданий), между которыми необходимо организовать постоянный информационный обмен, стационарно соединенные специально предназначенными для этих целей кабелями. Благодаря относительно небольшим длинам линий связи, по локальной сети можно передавать информацию в цифровом виде с высокой скоростью. Сеть указанного типа называется локальной вычислительной сетью (ЛВС) или по-английски LAN - Local Area Net .

Распределенная сеть объединяет значительно удаленные друг от друга компьютеры (например, расположенные в разных концах города или в разных городах), между которыми необходимо организовать постоянный обмен большими потоками информации; компьютеры в этих сетях соединяются специальными постоянно действующими выделенными каналами . Физически выделенные каналы могут реализовываться с помощью телефонных каналов или оптических кабелей, а также с помощью спутниковых или радиоканалов. С помощью выделенных каналов обычно соединяются удаленные компьютеры одной организации (например, компьютеры центрального офиса банка с компьютерами в его филиалах). Сети, связывающие значительно удаленные компьютеры, называются распределенными. Доступ к распределенным сетям организаций ограничен определенным кругом лиц, для которых работа в таких сетях связана с выполнением их должностных обязанностей. По своему функциональному назначению сети подобного типа эквиваленты локальным и называются региональными или по-английски Metropolitan Area Net - MAN .

Региональная сеть организации, в которой создана специальная коммуникационная система обмена сообщениями (электронная почта, факс, совместная работа над документами), называется корпоративной .

Глобальная сеть или Wide Area Net – WAN – это сеть компьютеров, распределенных по всему миру и постоянно связанных каналами с очень высокой пропускной способностью, на которых имеется большой объем разнообразной информации, доступной на коммерческой основе всем желающим.

Временная связь между удаленными ПК с помощью обычной телефонной сети через АТС может быть установлена с помощью устройства, называемого модемом (факс-модем). Такой способ связи называется связью по коммутируемому каналу . С помощью модема можно организовать информационный обмен между «обычными компьютерами», можно подключиться к локальной сети офиса или к глобальной сети.

Наряду с сетями, объединяющими несколько компьютеров, существуют сети терминалов, или терминальные сети , связывающие мощные компьютеры (мэйнфреймы) со специальными устройствами - терминалами, которые могут быть достаточно сложными, но вне сети их работа или невозможна, или вообще теряет смысл. Примерами терминальных устройств и терминальных сетей могут служить сеть банкоматов, сеть кассовых аппаратов в магазинах и др.